Energy Slaves reference list
This post is a reference list for the claims that I make in my non-fiction comic Energy Slaves. Toward the bottom, I also show my working for the statistics that I calculated myself, using other sources.
Page-by-page references
Firstly, here are sources for the specific claims that I make on certain pages of the comic:
- Pages 3-10: The ‘stuck in traffic’ part of the comic is merely a scenario that I developed to illustrate Buckminster Fuller’s ideas. I have no evidence that he actually had an epiphany during a traffic jam.
- Page 4: the ‘Leonardo da Vinci’ quote is attributed to Marshall McLuhan: Sieden (2012).
- Page 6: ‘100 harnessed horses jumping up and down’: Sieden (1989, p. 380).
- Page 9: Current generations are unfamiliar with farm animals in their daily lives. Sieden, (1989, pp. 353-4).
- Page 10: Statistics of ‘work per day by an average man’ being based on army data: Sieden, (1989, pp. 380–1). Bucky seems to have explained his logic in his book Nine Chains to the Moon (1938), which I have not read.(Although note below that during the making of this comic, I found that the data that Buckminster Fuller used was out by roughly a factor of ten.)See the ‘Errors made by Buckminster Fuller‘ section of this document for more info. In my comic, rather than use Bucky’s original—incorrect—figures, I have used the corrected versions.
- Pages 19-22: ’60 litre petrol tank’ / the work of 48 men / 4 energy slaves: see ‘workings’ section of this page. See also the description of the superhuman services provided by two jugs of gasoline in Hallett and Wright (2011, pp. 170–2).
- Pages 23-30: Description of humans gradually attracting more energy slaves from animals, wood, etc. From Heinberg (2003, pp. 48–60), Hallett and Wright (2011, pp. 33, 38, 75–82), Daly (1996, pp. 173, 177), Soddy (1926, pp. 29–31, 36), Soddy (1934, p. 163), Hopkins (2009, pp. 8–10).
- Page 28: Living within the ‘solar income’ budget available through daily sunshine. Fuller (1968, Chapter VIII, p. 79).
- Page 28: ‘Human ingenuity was merely redirecting solar flows’. All energy technologies indirectly harvest the sun’s energy. See Fuller (1968, Chapter VIII, p. 79). Bucky also mentions that we can harvest lunar power via tidal energy.
- Pages 31-2: Cars allowed human beings to make journeys that once took days in mere minutes. Sieden (1989, pp. 17-18). Bucky particularly referred to the ease in which he could make a daily commute to Harvard University, compared to his Fuller forebears.
- Pages 33-4: Jumbo jet on a Transatlantic flight: burning more fossil fuels than the whole continent of Europe used during the Stone Age. This is based on this quotation:
“a single B-17 bomber flying over Europe during WWII consumed more energy during one flight than the continent’s entire population had during the Stone Age.”
For this statistic, Andrew Nikiforuk (2012, p54) cites Leslie White’s “Energy and the evolution of culture” (American Anthripologist 45, no. 3 (1943): 335-356), which I have not read.
- Pages 43-4: The 4,000 kJ and 400 kJ numbers, relating to a drive to a convenience store are just round numbers that I use for example purposes.
- Page 46: Average late 20th century citizen enjoyed a slave count that ‘Spectacularly exceeded kings, queens and aristocrats’: Sieden (1989, pp. 380–1) and (Nikiforuk, 2012).
- Page 47: “a spending folly no less illogical than burning your house-and-home to keep the family warm on an unprecedentedly cold midwinter night” Fuller (1981, p. xvii).
- Page 48: Gasoline would be valued at $1 million per gallon, if we truly valued its preciousness. Fuller (1981, pp. xxxiv-xxxv, 200). Bucky is quoting geologist François de Chardenèdes on these pages of Critical Path.
- Page 49: “One year of human exercise (250 x eight-hour shifts) equals the energy-equivalent of 14 litres of gasoline.” See here for more info on the working of this statistic.
- Page 50: When I say that most motorists will burn 14 litres of fuel in one week, of course there are many motorists who will burn 14 litres in a day. (According to Fool.com, in 2017 the average American motorist used 656 gallons of gasoline per year. Via Wolfram Alpha this equals 6.8 litres per person per day. So, very close to 7 litres per person, per day.
In other words, one year of human effort would be required to generate the 14 litres of fuel that the average American motorist burns in two days of driving. (This statistic ignores the vast amounts of energy that is needed to support the person’s lifestyle in other ways. For example: farming the food that they eat, delivering parcels to their house, refrigerating their beer, powering the data centres that serve YouTube videos to their digital devices…). - Pages 65-6: Depth of the Drake Well (21.2 m) versus the depth of the Deepwater Horizon well (1,600 km of water + 4,000 km of crust): Ehrlich & Ehrlich (2014, p. 4). See also Wikipedia [1] [2]
- Page 66: “The Macondo oil field below the drilling platform contained a total volume of petroleum that would satisfy world oil consumption for only 12 hours.” See here for how I derived this statistc.
- Pages 67-8: Decline of ‘net energy’ from 100:1, down to 30:1, down to 10:1. This is also known as EROEI (Energy Returned on Energy Invested). Hopkins (2009, p45).
Sources listed above
- Ehrlich, Paul R.; Ehrlich, Anne H., 2014. Sustainable Futures: Linking Population, Resources and the Environment (edited by Jenny Goldie, Katharine Betts). CSIRO Publishing.
- Daly, Herman E., 1996. Beyond Growth: The Economics of Sustainable Development. Beacon Press.
- Dukes, J.S., 2003. Burning Buried Sunshine: Human consumption of ancient solar energy. Climatic Change 61, 31–44.
- Fuller, R. Buckminster, 1968. Operating manual for spaceship earth. Southern Illinois University Press.
- Fuller, R. Buckminster, 1981. Critical Path. St Martins Press.
- Hallett, Steve G.; Wright, John, 2011. Life Without Oil: Why We Must Shift to a New Energy Future. Prometheus Books.
- Heinberg, Richard, 2003. The Party’s Over: Oil, War and the Fate of Industrial Societies. New Society Publishers.
- Hopkins, Rob, 2009. The Transition Handbook: Creating local sustainable communities beyond oil dependency – Australia and New Zealand edition. Finch Publishing.
- Nikiforuk, Andrew, 2012. The Energy of Slaves: Oil and the New Servitude. Greystone Books.
- Sieden, Lloyd S., 1989. Buckminster Fuller’s Universe: His Life and Work. Perseus Publishing.
- Sieden, L. Steven, 2012. A Fuller View: Buckminster Fuller’s Vision of Hope and Abundance for All. Divine Arts.
- Soddy, Frederick, 1926. Virtual wealth and debt: the solution of the economic paradox. George Allen & Unwin.
- Soddy, Frederick, 1934. The role of money: what it should be, contrasted with what it has become. G. Routledge.
Workings for statistics quoted
Some of the statistics quoted in Energy Slaves are derived from other sources, which express the data in different ways.
Below is my working, so you can verify the mathematical logic I have used.
Energy Slaves:
A note about my use of the ‘Energy Slaves’ concept in this book.
I am aware of the wastefulness of many of our technologies. A classic example is the inefficiency of internal combustion energies: only a small percentage of the energy burnt is actually used to turn the vehicle’s wheels. The rest of the energy is squandered to useless ends, such as heating the engine block and exhaust pipe, as well as creating the audible sound energy of the engine running. This is a fact familiar to anyone who has heard a Harley-Davidson engine, or has burned themselves by accidentally touching the exhaust pipe with their bare skin.
It is true that we don’t truly “use” most of our slaves, and could therefore provide the services of many technologies with fewer slaves. A point brilliantly made by Natural Capitalism (1999) by Hawken, Lovins and Lovins.
However, for the purposes of this comic, I wanted to reveal the ultimate scale of the energy slaves on humanity’s payroll. The total number we send to work in the construction crew. A figure that includes those doing the digging, as well as those leaning on their shovels.
For tasks that are physically impossible for humans to perform (such as planes and cars, which require speeds far beyond Usain Bolt), I imagined the “work” of the energy slaves to be humanly-generating liquid fuel via exercise. Rather than actually pushing the vehicles, I imagined the energy slaves pedalling on stationary bikes, connected to some sort of electrolysis machine. Through their constant effort, the slaves would gradually create a quantity of fuel (e.g. liquid hydrogen) which could be instantaneously used in the same way that petrol can be used to fuel machines.
Naturally, it is more evocative for me to draw the hundreds and thousands of slaves actually pushing the vehicles in my artwork. However, I wanted to explain my deeper understanding of the physics and mathematics that lie behind this concept.
The ‘energy slave’ unit, as originally reported by Buckminster Fuller
My original source for Buckminster Fuller’s claimed workrate of an average healthy man is from the following quotation:
Buckminster Fuller originally quoted the daily statistic as:
150,000 foot-pounds of work in an eight hour day.—(Sieden, 1989, p. 380).
Converted from foot-pounds to SI units via Wolfram Alpha.
Equals 203.4 kJ or 0.2034 MJ per eight-hours of work.
Errors made by Buckminster Fuller
However, after talking to Energy Economics expert Olaf Schilgen, we think that Buckminster Fuller made a ‘decimal place error’. i.e. he should have included an extra zero at the end of his “150,000 foot-pounds of work” statistic that he quoted.
Bucky’s original statistic would have only been the equivalent of a human being expending 7 watts of energy continuously for 8 hours. That is far too low, as 7 W is the equivalent of a small light bulb.
70 watts is a more appropriate number. This is consistent with a 1983 paper on Bicycle Efficiency by Douglas Malewicki, which estimates that an average (non-athlete) “Healthy human” can sustain 75W during an 8 hour cycling period. (If it was only a 3 hour ride, Malewicki estimates that an average healthy human could expend about 150W, but only 75W is sustainable for 8 hours).
Revised units used from this point forward:
Rather than continuing with Buckminster Fuller’s original figures, which were wrong by a factor of 10, for all calculations further down this document, I will be using revised versions of Bucky Fuller’s calculations.
Also, instead of the archaic “foot-pounds of work” that Buckminster Fuller quoted, I will be using the SI units kilojoules (kJ) and megajoules (MJ).
Therefore, instead of using the original quoted statistic of 203.4 kilojoules – rounded-down to 200 kilojoules – we will use 2,000 kilojoules as our energy slaves output after an 8-hour work day. 2,000 kJ equals 2 MJ. We can also calculate hourly and yearly equivalents:
Hourly unit:
- 2,000 kJ divided by the 8 hours of the shift
- Equals an average of 250 kJ of work per hour (or 0.25 MJ per hour) across the 8-hour shift.
(As mentioned above, it would be possible for an average human to temporarily work at a higher output during a shorter shift, but 250 kJ per hour is what is considered sustainable for 8 hours by Malewicki.)
Yearly unit:
- 2,000 kJ multiplied by 250 working days across the year
- Equals 500 MJ of work per year. (This is ‘One energy slave‘, using Bucky’s definition).
Metric mass of a barrel of oil:
Each barrel of crude oil = 42 gallons = 158.97 Litres [via Wolfram Alpha]
- Converting volume into weight assuming specific gravity of 0.86 (Dukes, 2003, p. 38):
- 158.97 x 0.86 = 136.7142 kilograms = 0.1367142 tonnes.
Therefore we can say:
“One 42 US Gallon barrel of oil weighs 0.13 tonnes.”
Energy slaves in an barrel of oil:
For its calculation purposes, the International Energy Agency defines a “tonne of oil equivalent” as 107 kilocalories of energy per tonne (International Energy Agency, 2013, p. 21).
- This converts to 41.868 gigajoules of energy per tonne (International Energy Agency, 2013, p. 21).
- Each barrel of oil weighs 0.1367142 tonnes (see working above), so each barrel contains 41.868 x 0.13 = 5.72 gigajoules of energy.
- Converted into megajoules is 5720 MJ.
- Divided by 500 (the megajoule value of the annual work performed by Bucky Fuller’s ‘energy slave’ across 250 eight-hour shifts) equals 11.44.
Therefore we can say:
“Each barrel of oil, when burned, unlocked the services of over 11 energy slaves.”
Energy slaves in a litre of gasoline / petrol:
- Each barrel of motor gasoline contains 5,234,000 Btu of thermal energy (higher heating value) (“Annual Energy Outlook 2001: U.S. Energy Information Administration,” 2000, p. 251).
- Converted from British Thermal Units into metric via Wolfram Alpha: Each barrel of motor gasoline contains 5522 megajoules of energy.
- Divided by 158.97 Litres (volume of the ‘barrel’ unit) equals 34.736113732 megajoules of energy per litre of gasoline.
- {This corresponds with Hofstrand (2008, p. 1)}.
- Divided by 500 (the annual work of an ‘energy slave’), equals 0.069472227464.
Therefore, we can say:
“Each litre of gasoline / petrol, when burned, unlocked the service of approximately 0.07 energy slaves.”
Gasoline-equivalent amount of energy that can be generated by an energy slave:
Or, the reverse of the statistic above, we can calculate the gasoline-equivalent amount of energy that an average human can generate during one year.
- One human, working 8 hours per day for 250 days, can generate 500 MJ of energy.
- Each litre of gasoline contains 34.736113732 megajoules of energy.
- Divide 500 MJ by 34.736113732 = 14.39424121701284.
Therefore we can say: “an average man could only generate the energy-equivalent of 14 litres of gasoline each year”.
Energy slaves in a tank of gasoline / petrol:
Assuming a 60 litre fuel tank.
- 0.069472227464 multiplied by 60 equals 4.16833364784.
Therefore we can say:
“Each car’s 60 litre petrol tank…
…contains the energy equivalent of over 4 energy slaves.”
To make it seem like a more impressive quantity of slaves, we could multiply by 12 to get the number of ‘monthly slaves’. i.e.:
“When filled, each car’s 60 litre tank of gasoline contained an entire month’s work from 48 men.”
Burning a tank of gasoline in a single car trip:
An earlier version of Energy Slaves on pages 21-2 took the number of energy slaves contained within a 60 L petrol tank and divided it by a 9 hour drive. Here is the working for that statistic:
- 34.736113732 megajoules (energy per litre of gasoline) x 60 litres (fuel tank size) = 2084.16682392 megajoules of energy contained in a 60L fuel tank
- Burnt in a 9 hour drive = 231.574091547 megajoules of energy per hour
- Divided by 0.25 megajoules (the hourly work-rate of Bucky’s ‘healthy man’ derived from army statistics). Equals 926.296366188.
Therefore, we can say:
“Burned during a 9 hour drive, a 60 litre petrol tank conjures the strength of over 900 imaginary men to propel the car for the duration of the journey.”
Total energy contained in the Macondo Oil Field, beneath the BP Deepwater Horizon
“The Macondo oil field below the drilling platform contained a total volume of petroleum that would satisfy world oil consumption for only 12 hours.” (page 66)
I derived this statistic from the following data:
- Multiple web sources say that Macondo Prospect held 50 million barrels of oil total. [1] [2] [3]
- The International Energy Agency says that daily global oil consumption, as of 2016, is 96 million barrels. It is expected to rise above 100 million barrels per day by the end of this decade.
- 50 million is, thus, half of our daily consumption rate of 100 million barrels of oil.
- Therefore, based on these statistics, it seems that the Macondo Prospect only held about 12 hours worth of global oil consumption.
(Note that oil drillers typically only extract roughly 30-50% of the oil that is contained within oil fields. Therefore in a real-world scenario, the oil field would have realistically been able to power less than 6 hours of global consumption).
More essays from me about Energy Slaves
In addition to these references and calculations, I published some other essays that further explore the concepts of the Energy Slaves comic. Listed below are the seven articles:

Hidden in plain sight: our invisible slaves
Imaginary ‘energy slaves’ perform work on behalf of human beings. They are ‘hidden in plain sight’, because they make our lifestyles so effortless. Essay 1 / 7.
The mind, but not the muscle: understanding Energy Slaves
Did you know that an entire year of typical human exercise only equals the equivalent of 14 litres of gasoline (petrol). Energy powers our human lifestyles. Essay 2 / 7.
Building up steam: our civilisation’s history of collecting energy slaves
Energy has allowed people to magnify their impact on the natural world. This essay charts human civilisation’s history of gathering energy from fossil fuels. Essay 3 / 7.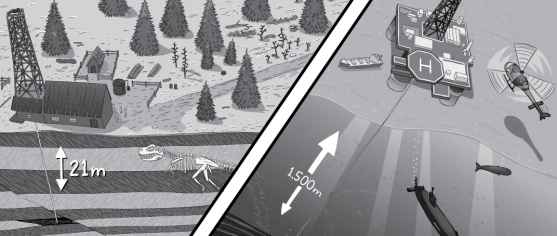
Diminishing returns: understanding ‘net energy’ and ‘EROEI’
At the heart of my Energy Slaves comic is the concept ‘EROEI’ (energy returned on energy invested) a.k.a. ‘net energy’. I explain this concept using the analogy of an apple orchard. Essay 4 / 7.
Powered by energy: the many layers of civilisation
Our civilisation has many layers, including industry, education, and healthcare. These layers are only possible because of fossil fuel energy surpluses. Essay 5 / 7.
Living within limits: low-energy lifestyles
Our lifestyles require vast amounts of energy. Will we be able to transition to low-energy alternatives that provide similar levels of happiness? Essay 6 / 7.
All part of the problem: our collective wastes of energy
It is easy to single out certain people for wasting energy. This essay discusses how we are all part of the problem. We all waste energy on a large scale. Essay 7 / 7.








Comments